Three-dimensional coordinate system

Sometime in the early 19th century the third dimension of measurement was added, using the z-axis.

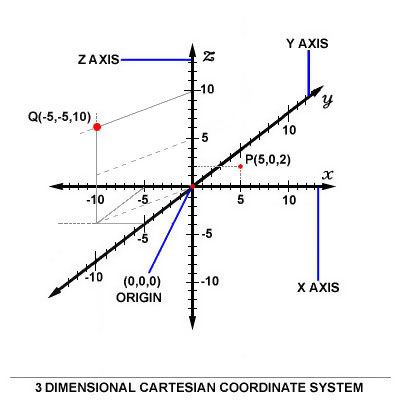
The coordinates in a three-dimensional system are of the form (x,y,z). An example of two points plotted in this system are in the picture above, points P(5, 0, 2) and Q(-5, -5, 10). Notice that the axes are depicted in a world-coordinates orientation with the z-axis pointing up.

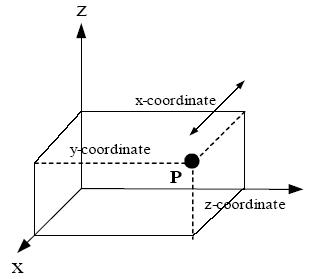
The x, y, and z coordinates of a point (say P) can also be taken as the distances from the yz-plane, xz-plane, and xy-plane respectively. The figure below shows the distances of point P from the planes.

The xy-, yz-, and xz-planes divide the three-dimensional space into eight subdivisions known as octants. While conventions have been established for the labeling of the four quadrants of the x'-y plane, only the first octant of three dimensional space is labeled. It contains all of the points whose x, y, and z coordinates are positive. That is, no point in the first octant has a negative coordinate. The three dimensional coordinate system is provides the physical dimensions of space � height, width, and length, and this is often referred to as "the three dimensions". It is important to note that a dimension is simply a measure of something, and that, for each class of features to be measured, another dimension can be added. Attachment to visualizing the dimensions precludes understanding the many different dimensions that can be measured (time, mass, color, cost, etc.). It is the powerful insight of Descartes that allows us to manipulate multi-dimensional object algebraically, avoiding compass and protractor for analyzing in more than three dimensions.

Orientation and "handedness"

The three-dimensional Cartesian coordinate system presents a problem. Once the x- and y-axes are specified, they determine the line along which the z-axis should lie, but there are two possible directions on this line. The two possible coordinate systems which result are called 'right-handed' and 'left-handed'.

The origin of these names is a trick called the right-hand rule (and the corresponding left-hand rule). If the forefinger of the right hand is pointed forward, the middle finger bent inward at a right angle to it, and the thumb placed a right angle to both, the three fingers indicate the relative directions of the x-, y-, and z-axes respectively in a right-handed system. Conversely, if the same is done with the left hand, a left-handed system results.

The right-handed system is universally accepted in the physical sciences, but the left-handed is also still in use.

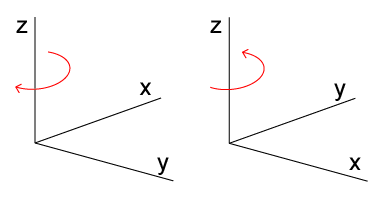
The left-handed orientation is shown on the left, and the right-handed on the right.

If a point plotted with some coordinates in a right-handed system is replotted with the same coordinates in a left-handed system, the new point is the mirror image of the old point about the xy-plane.

The right-handed Cartesian coordinate system indicating the coordinate planes.

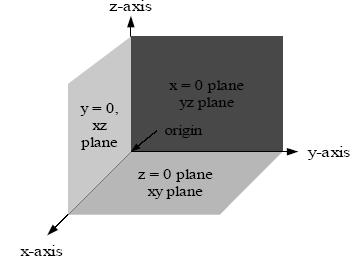
More ambiguity occurs when a three-dimensional coordinate system must be drawn on a two-dimensional page. Sometimes the z-axis is drawn diagonally, so that it seems to point out of the page. Sometimes it is drawn vertically, as in the above image (this is called a world coordinates orientation).

See also