View
A View as used in APAS/Wizard is a perspective projection of a
kinematic activity on a camera.
- A camera can be a real camera; in this case video is available:
video, strobe images, and data overlays can all be combined into one view.
- A camera can be a virtual camera; in this case there are no video
or strobe images available. The data can still be transformed and rendered
from any camera position.
View transformation
The view transformation locates the viewer in world space, transforming
vertices into camera space. In camera space, the camera, or viewer, is at the
origin, looking in the positive z-direction. The view matrix relocates the
objects in the world around a camera's position�the origin of camera space�and
orientation.
There are many ways to create a view matrix. In all cases, the camera has some
logical position and orientation in world space that is used as a starting point
to create a view matrix that will be applied to the models in a scene. The view
matrix translates and rotates objects to place them in camera space, where the
camera is at the origin. One way to create a view matrix is to combine a
translation matrix with rotation matrices for each axis. In this approach, the
following general matrix formula applies.
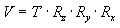
In this formula, V is the view matrix being created, T is a translation matrix
that repositions objects in the world, and Rx through Rz are rotation matrices
that rotate objects along the x-, y-, and z-axis. The translation and rotation
matrices are based on the camera's logical position and orientation in world
space. So, if the camera's logical position in the world is (10,20,100), the aim
of the translation matrix is to move objects -10 units along the x-axis, -20
units along the y-axis, and -100 units along the z-axis. The rotation matrices
in the formula are based on the camera's orientation, in terms of how much the
axes of camera space are rotated out of alignment with world space. For example,
if the camera mentioned earlier is pointing straight down, its z-axis is 90
degrees (pi/2 radians) out of alignment with the z-axis of world space, as shown
in the following illustration.
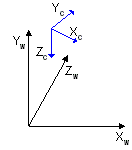
The rotation matrices apply rotations of equal, but opposite, magnitude to the
models in the scene. The view matrix for this camera includes a rotation of -90
degrees around the x-axis. The rotation matrix is combined with the translation
matrix to create a view matrix that adjusts the position and orientation of the
objects in the scene so that their top is facing the camera, giving the
appearance that the camera is above the model.
See also